Reply 1700 of 1969, by LewisWoolridge
I turns out that I had missed the instruction to first update to .92 before moving to .93. All is well now.
Thanks again Ronald!
I turns out that I had missed the instruction to first update to .92 before moving to .93. All is well now.
Thanks again Ronald!
Moving on to beta6:
All the latest files. To upgrade, just update dbgl.jar.
Ronald
Unless any serious issues pop up in the coming days, this might be the final beta before the next release. Any translators wanting to update their translations for the last changes, should check lines 125, 612 and 841-844.
Ronald
Hi everybody,
DBGL version 0.94 has been released, no changes since the last beta.
Ronald
Just got it installed here and the Dark Mode looks a bit off. My Mac has been in 'dark mode' since it became an option, and DBGL is a much lighter shade of grey than the OS GUI. If I leave it on the default, it matches MacOS exactly. Had two crashes too switching between the modes just now, no errors, the app just 'went away' after switching the pref and hitting the OK button. Everything else is great as usual. Now if I could only figure out why DOSBox-X is making every CGA machine come up blue Id be set!
The new 'Dark Mode' is meant for Windows users only (the colors should match those used in Eclipse) ; DBGL has supported dark mode on Mac and Linux platforms for a while now (ever since it was integrated in SWT).
If you exprience crashes, please start DBGL from inside a terminal; that will likely produce a stacktrace which I can analyze.
I've problem when importing D-Fend Reloaded profiles to DOSBox Game Launcher: The main folder of the games profile is "D:\Old_D\DOSBOX\D-Fend Reloaded\VirtualHD\FREEDOS" instead of the game folders:
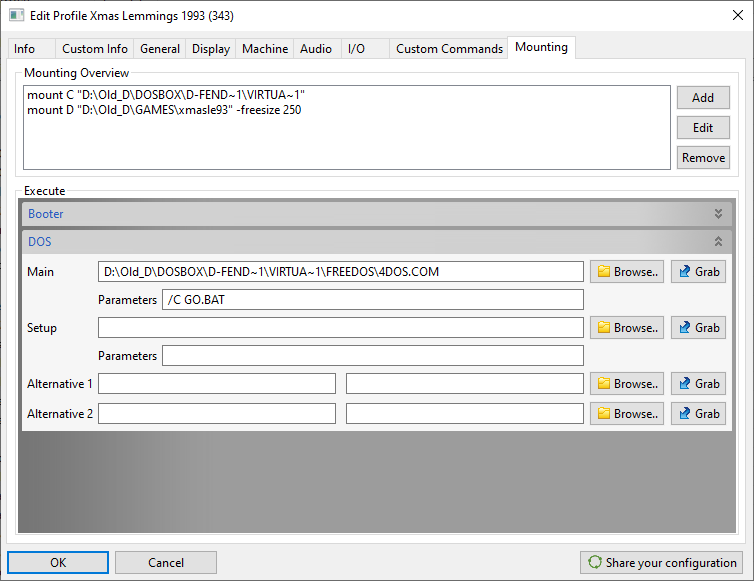
So I need to pass every profile and correct the main folder and file to the game file.
DOSBox 0.74-3
D-Fend Reloaded 1.4.4
DOSBox Game Launcher v0.97
Windows 10 Enterprise 64-bit version 22H2
dor123 wrote on 2021-08-29, 08:52:I've problem when importing D-Fend Reloaded profiles to DOSBox Game Launcher: The main folder of the games profile is "D:\Old_D\DOSBOX\D-Fend Reloaded\VirtualHD\FREEDOS" instead of the game folders...
Hi dor123,
Generally speaking, DBGL will try to keep the paths like they were in DFR. If you had your DFR games located inside "D:\Old_D\DOSBOX\D-Fend Reloaded\VirtualHD", DBGL will also use that location. What you can do with DBGL after importing the DFR profiles, is to use the 'migrate' function (Profiles -> Migrate profiles). Enter "D:\Old_D\DOSBOX\D-Fend Reloaded\VirtualHD" as "From" location and let DBGL process all profiles. After this, move all your games into DBGL's dosroot folder and you're done.
Having said that, your use-case seems a bit different, as you seem to have 2 paths configured?! Are all your games actually located inside D:\Old_D\GAMES ? And were they as such configured in DFR? Maybe you can share a screenshot of the paths configuration in DFR? I guess this problem might have something to do with using 4DOS...
All of my games located on D:\Old_D\GAMES\ and they were configurated such in DFR:
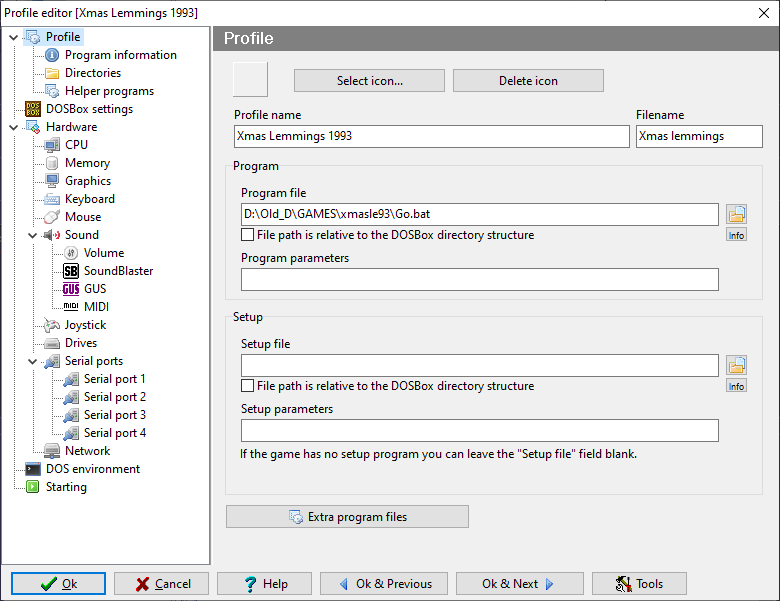
DOSBox 0.74-3
D-Fend Reloaded 1.4.4
DOSBox Game Launcher v0.97
Windows 10 Enterprise 64-bit version 22H2
rcblanke wrote on 2021-08-26, 15:07:The new 'Dark Mode' is meant for Windows users only (the colors should match those used in Eclipse) ; DBGL has supported dark mode on Mac and Linux platforms for a while now (ever since it was integrated in SWT).
If you exprience crashes, please start DBGL from inside a terminal; that will likely produce a stacktrace which I can analyze.
Hah well that explains that one. When I first saw the announcement I thought to myself 'its BEEN in dark mode for awhile now'. 😁
So far everything's been great, if I see any more Ill make sure I log it!
Hi folks,
Playing around with the launcher, and cannot find info on the following:
Is it possible to copy/clone templates? I want to make variations of existing ones, but cannot find a way to do it from the GUI. I tired manually copying one, but it does not show up automatically and I dont know what to modify to get it to show up (if that's even an option).
Thanks.
Just right-click on an existing template and select "Duplicate"!
rcblanke wrote on 2021-09-01, 07:51:Just right-click on an existing template and select "Duplicate"!
duplicate.png
Yeah, I just found it and feeling pretty stupid...
Thanks!
Bonus dumb Q: I know it's not DBGL specific, but is there any option to enable scanlines?
Edit: btw, are all those templates I see in the pic in some newer version or downloadable somewhere?
walterg74 wrote on 2021-09-01, 07:59:btw, are all those templates I see in the pic in some newer version or downloadable somewhere?
These are the default templates coming with DBGL since version 0.77. You didn't get them installed? Please try Templates -> Import default templates. If that doesn't work, please try running DBGL from a terminal window and check if there's any error messages showing up. Maybe the file dbgl/templates/default.xml is missing.
it is be possible to add for more configs based on the dosbox client like ECE and X? it would be great for a quick windows install like 3.11 up to 98.
rcblanke wrote on 2021-09-01, 12:36:walterg74 wrote on 2021-09-01, 07:59:btw, are all those templates I see in the pic in some newer version or downloadable somewhere?
These are the default templates coming with DBGL since version 0.77. You didn't get them installed? Please try Templates -> Import default templates. If that doesn't work, please try running DBGL from a terminal window and check if there's any error messages showing up. Maybe the file dbgl/templates/default.xml is missing.
So, while I was using a pack (still was v 0.82), I did just download the zip for v 0.94 but there is nothing in the templates folder besides the default.xml file (which is in fact there).
Import default templates works however, so I did get them. Just seems they were not in the zip.
rcblanke wrote on 2021-09-01, 12:36:walterg74 wrote on 2021-09-01, 07:59:btw, are all those templates I see in the pic in some newer version or downloadable somewhere?
These are the default templates coming with DBGL since version 0.77. You didn't get them installed? Please try Templates -> Import default templates. If that doesn't work, please try running DBGL from a terminal window and check if there's any error messages showing up. Maybe the file dbgl/templates/default.xml is missing.
Hi rcblanke, on an unrelated note, is there any documentation anywhere I could read to know the options, featurs, etc. better?
walterg74 wrote on 2021-09-02, 04:53:So, while I was using a pack (still was v 0.82), I did just download the zip for v 0.94 but there is nothing in the templates folder besides the default.xml file (which is in fact there).
Import default templates works however, so I did get them. Just seems they were not in the zip.
Not sure what you mean exactly, as default.xml actually contains all the data needed to create the 'default templates'. Normally, on first startup, DBGL will create these templates using the contents of default.xml. Somehow that must have failed on your DBGL installation, but at least good to hear that using the menu option succesfully created them anyway.
walterg74 wrote on 2021-09-02, 23:28:Hi rcblanke, on an unrelated note, is there any documentation anywhere I could read to know the options, featurs, etc. better?
All documentation on DBGL is located at the website. If you find you miss anything, just let me know.
DOSBox documentation can be found in the Manual, the website and the Wiki, mainly. Configuration options are documented in dosbox.conf.
rcblanke wrote on 2021-09-03, 14:23:Not sure what you mean exactly, as default.xml actually contains all the data needed to create the 'default templates'. Normally […]
walterg74 wrote on 2021-09-02, 04:53:So, while I was using a pack (still was v 0.82), I did just download the zip for v 0.94 but there is nothing in the templates folder besides the default.xml file (which is in fact there).
Import default templates works however, so I did get them. Just seems they were not in the zip.Not sure what you mean exactly, as default.xml actually contains all the data needed to create the 'default templates'. Normally, on first startup, DBGL will create these templates using the contents of default.xml. Somehow that must have failed on your DBGL installation, but at least good to hear that using the menu option succesfully created them anyway.
walterg74 wrote on 2021-09-02, 23:28:Hi rcblanke, on an unrelated note, is there any documentation anywhere I could read to know the options, featurs, etc. better?
All documentation on DBGL is located at the website. If you find you miss anything, just let me know.
DOSBox documentation can be found in the Manual, the website and the Wiki, mainly. Configuration options are documented in dosbox.conf.
Thanks!!!
Yes, I guess it´s because that pack I was using was already like that, prelaunched, and presumably ¨cleaned up¨, while the newer version (without knowing they are created on startup) I simply looked inside the zip file when I said they were not there.
Regarding the docs, I did go to the website, see many sections including some tutorials, etc. but was wondering if there was like a manual, or something like that to read. Maybe I missed a section or link but did not see it.
Thanks again!
Hi all,
I've made another GamePackArchive (338MB) (mirror) available for testing; the sixth collection of freeware, shareware and demo games as reviewed in ADG, episodes 259 to 290. It contains the following games:
Adventure
Blockout
Desert Strike: Return to the Gulf
Dominus
Gods
Inner Worlds
Jungle Strike
Labrynth of Zeux
Magus
Realms of the Haunting
SWIV 3D
The Black Cauldron
The Fortress of Dr. Radiaki
Theme Hospital
Toonstruck
Transland
Transport Tycoon Deluxe
Zork Nemesis: The Forbidden Lands
Most are shareware/demo versions. Comments and suggestions are welcome!